Aeroelasticity Phenomenon

This project deals with the interaction of wind with the elastic characteristics of a structure, which enables the structure to take energy from the wind and to vibrate. Under the condition called resonance, the structure will oscillate wildly. Forced resonance will be demonstrated in this experiment. This idea has been erroneously connected to the catastrophic failure of a bridge in 1940, the infamous Tacoma Narrows Bridge Disaster (seen below).

The extreme motion of the bridge shown above is much more complex than what we will explore in this experiment, though the experiment has some elements of the bridge phenomenon. The bridge failure was the result of torsional flutter. Torsion means twisting motion, and flutter can be explained as unstable vibration caused by aerodynamic forces.

Figure 1 Tacoma Narrows Bridge Disaster

Technical Discussion

The project uses the combined technologies of fluid dynamics and structures. In fluid dynamics, use is made of the Von Karman vortex street. The street is a series of vortices or swirling motions that are shed from a cylinder immersed in a fluid flow. (The fluid may be either gas or liquid, but for our purpose, only air will be considered). The shedding is the result of the inability of the fluid to completely follow the contour of the cylinder as a result of fluid viscosity. For a certain range of air stream velocities and cylinder diameters, the shedding has a regular frequency, and hence, can serve as the excitation of a structure. A wooden circular cylinder will represent the Tacoma Narrows Bridge in the experiment. The flow around a cylinder, and the vortex shedding, is shown in Figure 2.

Figure 2

Theoretical development for air flow over a cylinder.

The frequency of the shedding of the vortices related to the velocity of air flowing over a cylinder is given in Equation 1.

Equation 1

where f = frequency of shed vortices, rad/sec, V = airstream velocity, in/sec, and d equals cylinder diameter, inches. Thus, by inserting a cylinder of diameter d inches into an airstream flowing at V inches/second we will shed vortices at a frequency, f, of radians/second. To complete our system, we build a cylinder that is supported in the flow by a spring. This can be represented diagrammatically as:

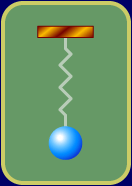
Figure 3

The suspended cylinder will oscillate at a frequency determined by the mass, m, of the cylinder and the stiffness of the spring (k):

Equation 2

where Equation. The spring stiffness has units lb/inch.

Experiment

Equipment needed to conduct this experiment:

Fan or blower capable of generating a range of air velocities
Several wooden cylinders of diameters between 0.5 and 3 inches
One or more sets of four springs, each with stiffness ranging from 0.5 to 18 lb/inch

The hardware that is used in the experiment is shown in Figure 4:

Figure 4

The fan provides the air stream that excites the spring-mounted cylinder. The four springs are attached to the cylinder on top and bottom near each end of the cylinder. The attachment can be made using eye hooks. The cylinder length should be enough so that it spans the exit nozzle of the fan. The ends of the springs that are not attached to the cylinder are to be attached to the rigid support frame. The frame must be strong enough not only to hold the cylinder in front of the fan, but also to hold it when it is bouncing (caused by the air flow over the cylinder).

What is required to complete the experiment is to size the hardware so that the frequencies of the shed vortices and the spring-mass system coincide. In order to apply the equation for the natural frequency of the spring-mass system, we will need an equivalent stiffness of four springs. This has been done and incorporated into Figure 5. The spring constant shown in Figure 5 is for one spring. You can measure this for any spring you might use by supporting one end of the spring and adding a known weight. Measuring the deflection will yield the spring constant by taking the slope of the straight line that results. For a range of spring constants and cylinder diameters that are readily purchased, the flow velocity that is required out of the fan is shown in Figure 5.

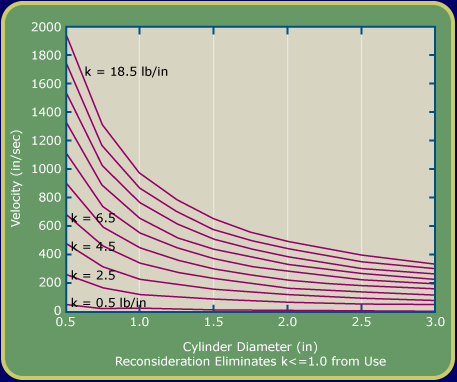
Figure 5

An alternative to measuring the velocity of the flowing air is to measure the pressure of the airstream as it is brought to rest. This is called the total pressure. It can be measured by an airstream as it is brought to rest. An apparatus, as shown in Figure 6, can measure total pressure. This device uses the principle of Bernoulli’s law to relate the pressure of the moving air stream as it is brought to a rest in the total head probe. The speed of the airstream will vary over the entire area of the fan so the velocity should be measured at the front of the cylinder.

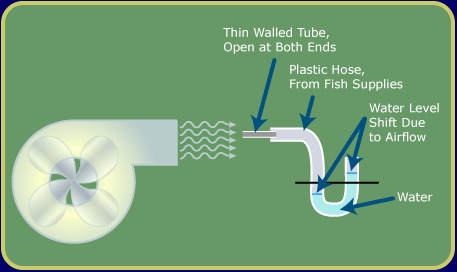
Figure 6

The preceding graph, Figure 5, becomes:

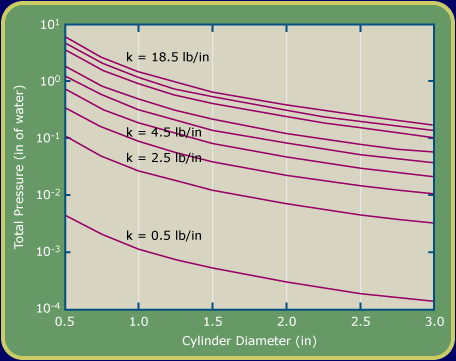
Figure 7

The velocity of the air must be “in the ballpark” of the values shown in the Figure 5. Alternately, the airstream pressure must be “in the ballpark”of the values shown in Figure 7. The cylinder will oscillate at a frequency in accordance with Equation 1 and the cylinder diameter also shown on the graphs. When the frequency of the excitation from the moving air stream is the same as the natural frequency of the cylinder/spring (“spring-mass”) system, resonance occurs and the system will oscillate wildly.

Measurements

Spring constant
Air velocity
Cylinder oscillation as a function of airspeed for fixed cylinder diameter
Cylinder oscillation as a function of cylinder diameter for fixed airspeed
Frequency of oscillation of the spring-mass system for various springs and weights

References

Billah, K.Y., Scanlan, R. H. “Resonance, Tacoma Narrows Bridge Failure, and Undergraduate Physics”, American Journal of Physics, 59 (2), February 1992
Schlicting, H. “Boundary Layer Theory”, Mcgraw-Hill Book Co. New York, 1960

Click here for a printable version of this experiment Click Here